LEDNINGER.

Strømledninger er vanligvis laget av kopper eller aluminium. Disse metallene har lav resistivitet, og de kan derfor føre ganske store strømmer uten å bli særlig varme. Samtidig har slike metaller et høyt smeltepunkt. Det skal mye elektrisk strøm til før en blank leder blir skadet av varmeutvikling.

Isolasjonen, som befinner seg rundt lederne, er laget av mer følsomme stoffer. Her brukes det ofte forskjellige typer plast eller gummistoffer. Slike stoffer kan skades ved for høye temperatur.

Isolasjonen setter grenser for hvor stor strømføring en ledning kan ha. Den elektriske strømmen skaper varme inne i lederen. Varmen må ledes ut gjennom isolasjonen før den kan bli avgitt til omgivelsene. Dermed får lederen en bestemt evne til å lede strøm. Denne evnen er avhengig av flere faktorer.:

1.: Hva slags materiale lederen er laget av.

2.: Hvor stort tverrsnitt lederen har.

3.: Hvor stor temperatur isolasjonen tåler.

4.: Ledningens muligheter til å avgi varmen til omgivelsene.

LEDNINGENS RESISTANS.

Ledningens resistans er avhengig av resistiviteten på ledermaterialet, lengda på-, og arealet til lederen. Resistansen i en kabel kan regnes ut med følgende formel.:

Rk = Resistansen i fram og tilbakeføringa for enfasekabel.

r = Resistiviteten for stoffet ved 30 gr. C.

L = Lengda på kabelen.

A = Tverrsnittet på kabelen.

Ledningens resistans er avhengig av temperaturen. Formelen beregner resistansen når temperaturen på ledningen er 30 o C. Ved høyere temperaturer, vil resistansen bli større. Dette er det viktig å være klar over når man arbeider med deler av forskriftene.

EFFEKTTAPET I EN KABEL.

Når det går en strøm gjennom en kabel, vil det også bli utviklet effekt i denne. Effektutviklinga kan finnes ved hjelp av denne kjente formelen: (Formelen gjelder både for veksel- og likestrøm. )

P_k = I² × R_k

P_{k =} Effektutviklinga i kabelen.

I = Belastningsstrømmen.

R_{k =} Resistansen i kabelen.

Det er dette effekttapet som bestemmer kabelens arbeidstemperatur under drift.

KABELENS KAPASITIVE MOTSTAND:

Likestrømsanlegg kan man se bort fra denne typen motstand. De to strømførende lederne i en kabel har en spesiell lengde og diameter. De er isolert fra hverandre med et isolasjonsstoff.

Dette fører til at kabelen blir en kondensator, og at den kan lades opp med elektrisk ladning mellom de to lederne.

Kapasitansen mellom fasene kalles for Cl. Denne har liten praktisk betydning for de normale kabelanleggene som installereres i bygninger. Kapasiteten er så liten at det ikke kan bygge seg opp farlige ladninger.

På høyspentanlegg er dette annerledes. Der kan Cl inneholde livsfarlige ladninger selv om linjene er koplet ut.

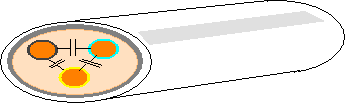
De fleste kabler inneholder en jordledning. Jordlederen danner også et areal mot faselederen samtidig som også disse er isolert fra hverandre Dermed blir det dannet en kondensator mellom faselederne og jord. Jordkappasiteten i et kabelanlegg kalles for Cj.

KABELENS MAGNETISKE MOTSTAND: (INDUKTANS)

Når det går strøm gjennom en ledning, blir det også satt opp et magnetfelt rundt denne. Retningen på feltet er avhengig av hvilken vei strømmen går i ledningen.

Dersom ledningen blir utsatt for vekselstrøm, fører dette til en kontinuerlig skifting av polariteten på magnetfeltet rundt kabelen. Dermed oppstår det induksjon i selve ledningen.

Dette fenomenet kalles for INDUKTIV REAKTANS. Det betyr at ledningen selv prøver å lage en strøm som motvirker den strømmen som ledningen egentlig skal føre.

KABELENS REGNESKJEMA.

Den strømmen som går gjennom en kabel, vil møte tre former for motstand. Dersom man skal regne på en overføring, er det til god hjelp å kunne tegne opp et regneskjema. Regneskjemaet skal inneholde de komponentene som blir tatt med i beregningen.

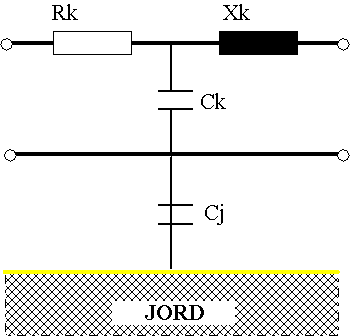
I regneskjemaet ser vi hvordan resistansen, den induktive reaktansen og kapasiteten kan danne en strømkrets.

Kapasitansen virker jevnt over hele kabelens lengde. Derfor er det naturlig å dele denne inn som to kondensatorer. Disse bør tegnes inn i hver ende på kabelen.

Rk = Kabelens resistans.

Xk = Kabelens induktive reaktans

Ck = Kapasitansen mellom lederne.

Cj = Kapasitansen mellom lederne og jord.

TABELL FOR KABLERS ELEKTRISKE DATA.

Tabellen viser en del elektriske data for enkelte normale installasjonskabler med PVC-isolasjon. Kabelens induktive reaktans er regnet ut for 50 Hz, og denne er oppgitt i mW / m.

Kapasitansen er oppgitt i nF/m. Ved hjelp av denne er det tilnærmet mulig å beregne den kapasitive tomgangsstrømmen som kabelen trekker, og den jordlekkstrømmen som er tilstede i anlegget.

Cl = Kapasitansen mellom lederne.

Cj = Kapasitansen mellom en leder og jord.

Resistansen er oppgitt i mW / m for massive ledere av kopper (Cu) ved 20 C.

TVERSNITT	RESISTANS	KAPASITANS		INDUKTIV REAKTANS
		Cl	Cj
1,5 mm^2	12,1 mW / m	0,35 nF / m	0,64 nF / m	0,10 mW / m
2,5 mm^2	7,41 mW / m	0,40 nF / m	0,72 nF / m	0,10 mW / m
4 mm^2	4,61 mW / m	0,42 nF / m	0,80 nF / m	0,10 mW / m
6 mm^2	3,08 mW / m	0,46 nF / m	0,85 nF / m	0,09 mW / m
10 mm^2	1,83 mW / m	0,53 nF / m	0.97 nF / m	0,09 mW / m
16 mm^2	1,15 mW / m	0,59 nF / m	1,10 nF / m	0,08 mW / m
25 mm^2	0,73 mW / m	0,69 nF / m	1,25 nF / m	0,08 mW / m
35 mm^2	0,52 mW / m	0,79 nF / m	1,40 nF / m	0,08 mW / m
50 mm^2	0,39 mW / m	0,90 nF / m	1,60 nF / m	0,07 mW / m
120 mm^2	0,15 mW / m	0,95 nF / m	1,75 nF / m	0,07 mW / m
240 mm^2	0,08 mW / m	1,05 nF / m	1,92 nF / m	0,07 mW / m

OPPVARMING AV KABLER.

Når kabelen blir utsatt for kortslutningstrømmer, blir den ganske fort skadelig oppvarmet. Denne kurven viser hvor lenge en kortsluttningstrøm kan være tilstede i en kabel før denne tar varig skade av det.

KURVE