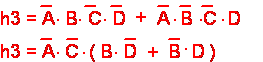Digital matematikk.
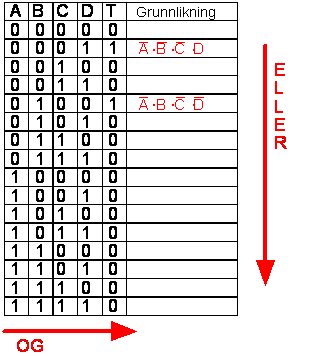
Man kan sette opp en grunnlikning ved hjelp av en sannhetstabell. Grunnlikningen viser oss hvordan styringen kan kobles for å få til den responsen som vi ønsker at lampen skal ha på bryterne.
	Det eksemplet vi har valgt ut fra heisen, gir oss følgende grunnlikning.
	Denne likningen kan vi uten videre koble opp gjennom de forskjellige bryterne som finnes i heisen. Lampen får nå den responsen som vi ønsker oss.
Men det kan være mulig at denne koblingen kan utføres noe enklere, og likevel gjøre samme jobben. Vi har nå satt opp en likning, og vi kan bruke litt av den vanlige mattematikken på denne likningen. Det får vi til ved å lage en parentes.
Dersom du ser på 2 ledd i en slik grunnlikning, vil du ofte finne at enkelte brytere blir like i begge leddene. Da er det mulig å sette disse like bryterne utenfor en parentes.
Dermed forandrer du kretsen slik at du kan oppnå det samme ved hjelp av litt mindre brytere. Dersom du tenker på at en bryterkontakt koster 100 Kr., så ser du nå at du har spart 200 Kr.
Her ser du at det utrykket som du får inne i parentesen, danner en eksklusiv eller funksjon.